6.3 Operaciones básicas con árboles:  

Salvo que trabajemos con árboles especiales, como los que veremos más adelante, las inserciones serán siempre en punteros de nodos hoja o en punteros libres de nodos rama. Con estas estructuras no es tan fácil generalizar, ya que existen muchas variedades de árboles.

De nuevo tenemos casi el mismo repertorio de operaciones de las que disponíamos con las listas:

• Añadir o insertar elementos.
• Buscar o localizar elementos.
• Borrar elementos.
• Moverse a través del árbol.
• Recorrer el árbol completo.

Los algoritmos de inserción y borrado dependen en gran medida del tipo de árbol que estemos implementando, de modo que por ahora los pasaremos por alto y nos centraremos más en el modo de recorrer árboles.

6.4 Recorridos por árboles:  

El modo evidente de moverse a través de las ramas de un árbol es siguiendo los punteros, del mismo modo en que nos movíamos a través de las listas.

Esos recorridos dependen en gran medida del tipo y propósito del árbol, pero hay ciertos recorridos que usaremos frecuentemente. Se trata de aquellos recorridos que incluyen todo el árbol.

Hay tres formas de recorrer un árbol completo, y las tres se suelen implementar mediante recursividad. En los tres casos se sigue siempre a partir de cada nodo todas las ramas una por una.

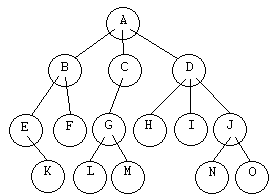
Supongamos que tenemos un árbol de orden tres, y queremos recorrerlo por completo.

Partiremos del nodo raíz:

RecorrerArbol(raiz);

La función RecorrerArbol, aplicando recursividad, será tan sencilla como invocar de nuevo a la función RecorrerArbol para cada una de las ramas:

void RecorrerArbol(Arbol a) {
   if(a == NULL) return;
   RecorrerArbol(a->rama[0]);
   RecorrerArbol(a->rama[1]);
   RecorrerArbol(a->rama[2]);
}

Lo que diferencia los distintos métodos de recorrer el árbol no es el sistema de hacerlo, sino el momento que elegimos para procesar el valor de cada nodo con relación a los recorridos de cada una de las ramas.

Los tres tipos son:

Pre-orden:

En este tipo de recorrido, el valor del nodo se procesa antes de recorrer las ramas:

void PreOrden(Arbol a) {
   if(a == NULL) return;
   Procesar(dato);
   RecorrerArbol(a->rama[0]);
   RecorrerArbol(a->rama[1]);
   RecorrerArbol(a->rama[2]);
}

Si seguimos el árbol del ejemplo en pre-orden, y el proceso de los datos es sencillamente mostrarlos por pantalla, obtendremos algo así:

A B E K F C G L M D H I J N O

In-orden:

En este tipo de recorrido, el valor del nodo se procesa después de recorrer la primera rama y antes de recorrer la última. Esto tiene más sentido en el caso de árboles binarios, y también cuando existen ORDEN-1 datos, en cuyo caso procesaremos cada dato entre el recorrido de cada dos ramas (este es el caso de los árboles-b):

void InOrden(Arbol a) {
   if(a == NULL) return;
   RecorrerArbol(a->rama[0]);
   Procesar(dato);
   RecorrerArbol(a->rama[1]);
   RecorrerArbol(a->rama[2]);
}

Si seguimos el árbol del ejemplo en in-orden, y el proceso de los datos es sencillamente mostrarlos por pantalla, obtendremos algo así:

K E B F A L G M C H D I N J O

Post-orden:

En este tipo de recorrido, el valor del nodo se procesa después de recorrer todas las ramas:

void PostOrden(Arbol a) {
   if(a == NULL) return;
   RecorrerArbol(a->rama[0]);
   RecorrerArbol(a->rama[1]);
   RecorrerArbol(a->rama[2]);
   Procesar(dato);
}

Si seguimos el árbol del ejemplo en post-orden, y el proceso de los datos es sencillamente mostrarlos por pantalla, obtendremos algo así:

K E F B L M G C H I N O J D A

6.5 Eliminar nodos en un árbol:  

El proceso general es muy sencillo en este caso, pero con una importante limitación, sólo podemos borrar nodos hoja:

El proceso sería el siguiente:

1. Buscar el nodo padre del que queremos eliminar.
2. Buscar el puntero del nodo padre que apunta al nodo que queremos borrar.
3. Liberar el nodo.
4. padre->nodo[i] = NULL;.

Cuando el nodo a borrar no sea un nodo hoja, diremos que hacemos una "poda", y en ese caso eliminaremos el árbol cuya raíz es el nodo a borrar. Se trata de un procedimiento recursivo, aplicamos el recorrido PostOrden, y el proceso será borrar el nodo.

El procedimiento es similar al de borrado de un nodo:

1. Buscar el nodo padre del que queremos eliminar.
2. Buscar el puntero del nodo padre que apunta al nodo que queremos borrar.
3. Podar el árbol cuyo padre es nodo.
4. padre->nodo[i] = NULL;.

En el árbol del ejemplo, para podar la rama 'B', recorreremos el subárbol 'B' en postorden, eliminando cada nodo cuando se procese, de este modo no perdemos los punteros a las ramas apuntadas por cada nodo, ya que esas ramas se borrarán antes de eliminar el nodo.

De modo que el orden en que se borrarán los nodos será:

K E F y B

6.6 árboles ordenados:  

A partir del siguiente capítulo sólo hablaremos de árboles ordenados, ya que son los que tienen más interés desde el punto de vista de TAD, y los que tienen más aplicaciones genéricas.

Un árbol ordenado, en general, es aquel a partir del cual se puede obtener una secuencia ordenada siguiendo uno de los recorridos posibles del árbol: inorden, preorden o postorden.

En estos árboles es importante que la secuencia se mantenga ordenada aunque se añadan o se eliminen nodos.

Existen varios tipos de árboles ordenados, que veremos a continuación:

• árboles binarios de búsqueda (ABB): son árboles de orden 2 que mantienen una secuencia ordenada si se recorren en inorden.
• árboles AVL: son árboles binarios de búsqueda equilibrados, es decir, los niveles de cada rama para cualquier nodo no difieren en más de 1.
• árboles perfectamente equilibrados: son árboles binarios de búsqueda en los que el número de nodos de cada rama para cualquier nodo no difieren en más de 1. Son por lo tanto árboles AVL también.
• árboles 2-3: son árboles de orden 3, que contienen dos claves en cada nodo y que están también equilibrados. También generan secuencias ordenadas al recorrerlos en inorden.
• árboles-B: caso general de árboles 2-3, que para un orden M, contienen M-1 claves.